VBA Operators
VBA operators are special tokens that instruct the compiler to “operate” on values or program identifiers. They are also referred to as program symbols or code elements. Also, the program identifiers they operate on (e.g., addition) must be capable of holding values.
You may have heard of the term operand. These are the values (i.e., literals) or identifiers (e.g., variables and constants) that operators act on. Based on their number of operands, operators are either unary or binary.
Unary VBA operators are operators that only act on a single operand at a time. Binary VBA operators are those that only act on two operands at a time.
VBA supports the following categories of operators:
- Assignment Operator;
- Member Access Operators;
- Concatenation Operators;
- Arithmetic Operators;
- Comparison Operators;
- Logical Operators.
This article takes an in-depth look at the VBA arithmetic operators.
VBA Operator Precedence
Often, an operation involves more than one operator, sometimes of different categories. So, it is worthwhile paying special attention to the order of precedence of the VBA operators. Otherwise, VBA’s default operator precedence applies.
The default precedence is as follows: arithmetic first, then concatenation, followed by comparison, then logical, and finally assignment operators.
Moreover, there is a pre-set precedence for operators within each category. How do you override this default order and remove any ambiguity? Easy, set the preferred precedence with open and close parentheses, ( ).
Arithmetic Operators
Arithmetic operators perform simple mathematic operations. Their operations include addition, subtraction, division, multiplication, exponentiation and modulus. The table below summarizes the different VBA arithmetic operators.
| Operator | Description | Return Data Type | Order |
|---|---|---|---|
| ^ | Exponentiation (binary) operator, i.e. caret (^), raises a number to the power of an exponent. | Double or Double Variant (i.e., a Variant holding data of Double data type); Null, if one or each operand is a Null expression. | 1 |
| - | Negation (unary) operator, i.e. dash (-), turns a numeric value negative (or positive, if the value was already negative). | Most precise type for the result – precision increasing in the order: Byte, Integer, Long, Single, Double, Currency, and Decimal; Null, if the operand is a Null expression. | 2 |
| * | Multiplication (binary) operator, i.e. asterisk (*), returns the product of two numbers. | Most precise type for the result – precision increasing in the order: Byte, Integer, Long, Single, Currency, Double, and Decimal; Null, if one or each operand is a Null expression. | 3 |
| / | Division (binary) operator, i.e. forward-slash (/), returns the floating-point result of dividing two numbers. | Double or Double Variant; Null, if one or each operand is a Null expression. | 3 |
| \ | Integer Division (binary) operator, i.e. backslash (\), returns the result (with fractional part cut off) of dividing two numbers (first rounded to Byte, Integer, or Long, if floating-point). | Byte, Byte Variant, Integer, Integer Variant, Long, or Long Variant; Null, if one or each operand is a Null expression. | 4 |
| Mod | Modulus (binary) operator, Mod, returns the remainder (with fractional part cut off) from dividing two numbers (first rounded to Integer, if floating-point). | Byte, Byte Variant, Integer, Integer Variant, Long, or Long Variant; Null, if one or each operand is a Null expression. | 5 |
| + | Addition (binary) operator, i.e. plus (+), returns the sum of two numbers. | Most precise type for the result – precision increasing in the order: Byte, Integer, Long, Single, Double, Currency, and Decimal; Null, if operand is a Null expression; Integer, if both operands are Empty. | 6 |
| - | Subtraction (binary) operator, i.e. dash (-), returns the result of deducting one number from another. | Most precise type for the result – precision increasing in the order: Byte, Integer, Long, Single, Double, Currency, and Decimal; Null, if operand is a Null expression. | 6 |
When several arithmetic operators with the same precedence appear together in an expression, evaluation proceeds in the order of appearance from left to right. Also, enclosing a part of an expression in parentheses causes it to be evaluated ahead of other parts.
Arithmetic Operators: Exponentiation (^)
Always put a space character right before the exponentiation operator, ^, to ensure that the VBA editor correctly interprets it, even in 64-bit environments.
That is because the operator creates LongLong data types in 64-bit environments. So, a compile error is thrown without the space character immediately before it.
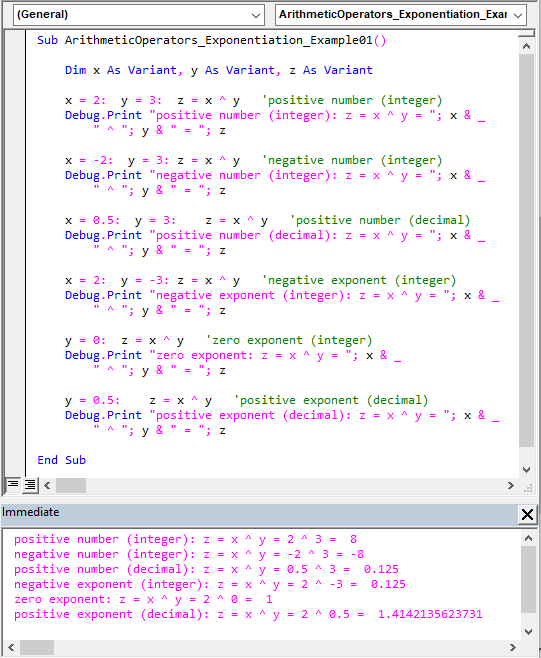
The sample code below demonstrates the exponentiation (^) operator’s usage.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 |
Sub ArithmeticOperators_Exponentiation_Example01() Dim x As Variant, y As Variant, z As Variant x = 2: y = 3: z = x ^ y 'positive number (integer) Debug.Print "positive number (integer): z = x ^ y = "; x & _ " ^ "; y & " = "; z x = -2: y = 3: z = x ^ y 'negative number (integer) Debug.Print "negative number (integer): z = x ^ y = "; x & _ " ^ "; y & " = "; z x = 0.5: y = 3: z = x ^ y 'positive number (decimal) Debug.Print "positive number (decimal): z = x ^ y = "; x & _ " ^ "; y & " = "; z x = 2: y = -3: z = x ^ y 'negative exponent (integer) Debug.Print "negative exponent (integer): z = x ^ y = "; x & _ " ^ "; y & " = "; z y = 0: z = x ^ y 'zero exponent (integer) Debug.Print "zero exponent: z = x ^ y = "; x & _ " ^ "; y & " = "; z y = 0.5: z = x ^ y 'positive exponent (decimal) Debug.Print "positive exponent (decimal): z = x ^ y = "; x & _ " ^ "; y & " = "; z End Sub |
Arithmetic Operators: Negation (-)
The order of precision used by addition, subtraction, and negation differ from that used by multiplication. In the summary table above, the difference is subtle but it should be noted.
Did you spot the swapped positions of Double and Currency data types for the multiplication operator? Why the cheeky swap? Beats me.
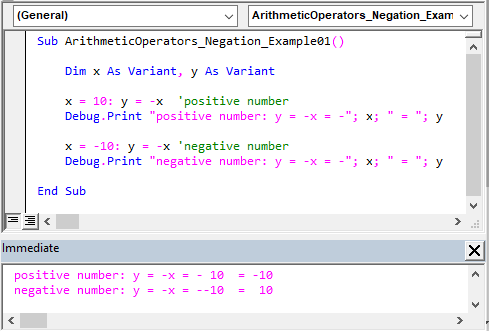
The sample code below shows the negation (-) operator’s usage.
|
1 2 3 4 5 6 7 8 9 10 11 |
Sub ArithmeticOperators_Negation_Example01() Dim x As Variant, y As Variant x = 10: y = -x 'positive number Debug.Print "positive number: y = -x = -"; x; " = "; y x = -10: y = -x 'negative number Debug.Print "negative number: y = -x = -"; x; " = "; y End Sub |
Arithmetic Operators: Multiplication (*), Division (/), and Integer Division (\)
The sample code below illustrates the multiplication (*), division (/), and integer division (\) operators’ usage.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 |
Sub ArithmeticOperators_Multiplication_Division_Example01() Dim x As Variant, y As Variant, z As Variant 'multiplication x = 2: y = 3: z = x * y Debug.Print "Multiplication: z = x * y = "; x & _ " * "; y & " = "; z x = 2.5: y = 3.5: z = x * y Debug.Print "Multiplication: z = x * y = "; x & _ " * "; y & " = "; z & vbCrLf 'division x = 8: y = 4: z = x / y Debug.Print "Division: z = x / y = "; x & _ " / "; y & " = "; z x = 14.5: y = 5: z = x / y Debug.Print "Division: z = x / y = "; x & _ " / "; y & " = "; z & vbCrLf 'integer division x = 14.4: y = 5: z = x \ y Debug.Print "Integral division: z = x \ y = "; x & _ " \ "; y & " = "; z x = 14.5: y = 5: z = x \ y Debug.Print "Integral division: z = x \ y = "; x & _ " \ "; y & " = "; z x = 14.6: y = 5: z = x \ y Debug.Print "Integral division: z = x \ y = "; x & _ " \ "; y & " = "; z End Sub |
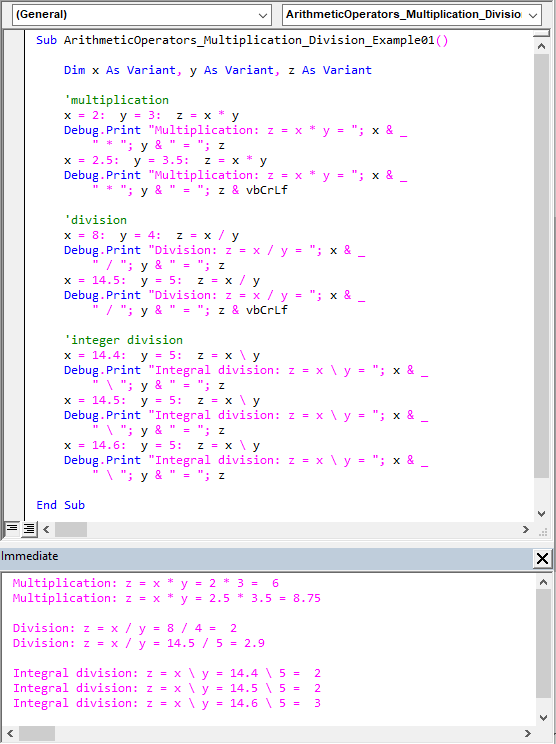
As shown in the sample code above, for integer division the operands are rounded to Byte, Integer, or Long values before the division occurs. So, “14.4 \ 5” and “14.5 \ 5” both equate to “14 \ 5” which yields ‘2’. However, “14.6 \ 5” equates to “15 \ 5” which yields ‘3.’
Moreover, comparing the results of “14.5 / 5” and “14.5 \ 5,” shows that integer division truncates the result’s fractional part. On the other hand, the normal division does not.
Arithmetic Operators: Modulus (Mod)
The sample code below demonstrates the modulus (Mod) operator’s usage.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
Sub ArithmeticOperators_Modulus_Example01() Dim x As Variant, y As Variant, z As Variant 'Modulus x = 5: y = 4: z = x Mod y 'integral numbers Debug.Print "Modulus: z = x Mod y = "; x & _ " Mod "; y & " = "; z x = 4: y = 5: z = x Mod y 'integral numbers Debug.Print "Modulus: z = x Mod y = "; x & _ " Mod "; y & " = "; z & vbCrLf x = 5: y = 3.4: z = x Mod y 'floating-point numbers Debug.Print "Modulus: z = x Mod y = "; x & _ " Mod "; y & " = "; z x = 5.8: y = 3: z = x Mod y 'floating-point numbers Debug.Print "Modulus: z = x Mod y = "; x & _ " Mod "; y & " = "; z & vbCrLf End Sub |
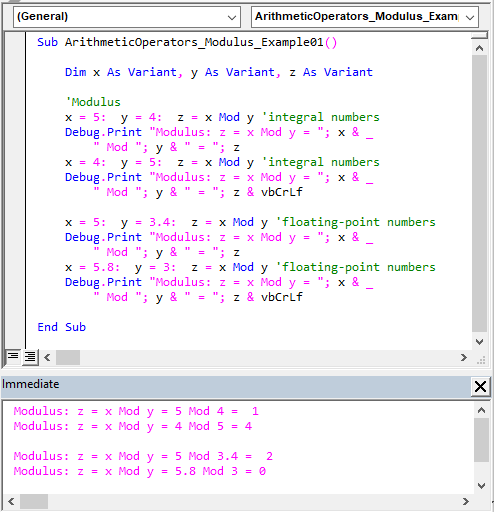
As shown in the sample code above, the modulus operator first rounds the operands (if floating-point or fractional values) to an Integer value before the dividing them and returning the remainder.
So, “5 Mod 3.4” equates to “5 Mod 3” which yields a remainder of ‘2.’ Likewise, “5.8 Mod 3” equates to “6 Mod 3” which yields a remainder of ‘0.’ Moreover, “4 Mod 5” yields ‘4’ as ‘5’ cannot divide into ‘4’ an integral number of times (i.e., “4 / 5” < 0).
Arithmetic Operators: Addition (+) and Subtraction (-)
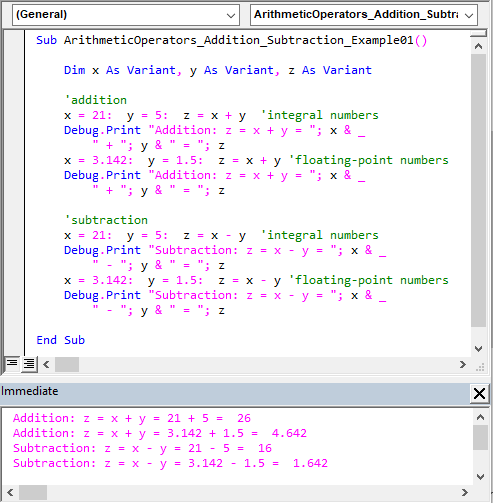
The sample code below shows the addition (+) and subtraction (-) operators’ usage.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
Sub ArithmeticOperators_Addition_Subtraction_Example01() Dim x As Variant, y As Variant, z As Variant 'addition x = 21: y = 5: z = x + y 'integral numbers Debug.Print "Addition: z = x + y = "; x & _ " + "; y & " = "; z x = 3.142: y = 1.5: z = x + y 'floating-point numbers Debug.Print "Addition: z = x + y = "; x & _ " + "; y & " = "; z 'subtraction x = 21: y = 5: z = x - y 'integral numbers Debug.Print "Subtraction: z = x - y = "; x & _ " - "; y & " = "; z x = 3.142: y = 1.5: z = x - y 'floating-point numbers Debug.Print "Subtraction: z = x - y = "; x & _ " - "; y & " = "; z End Sub |


![The While – Wend statement’s syntax. Square brackets, [ ], indicate optional items.](https://masterofficevba.com/wp-content/uploads/2021/03/While_Wend_Statement_Syntaxnew.png)
![The Do – Loop Until statement’s syntax. Square brackets, [ ], indicate optional items while vertical bars, |, indicate mutually exclusive items.](https://masterofficevba.com/wp-content/uploads/2021/03/Do_Loop_Until_Statement_Syntaxnew.png)
![The Do – Loop While statement’s syntax. Square brackets, [ ], indicate optional items while vertical bars, |, indicate mutually exclusive items.](https://masterofficevba.com/wp-content/uploads/2021/03/Do_Loop_While_Statement_Syntaxnew.png)
![The Do Until – Loop statement’s syntax. Square brackets, [ ], indicate optional items.](https://masterofficevba.com/wp-content/uploads/2021/03/Do_Until_Loop_Statement_Syntaxnew.png)





![The While – Wend statement’s syntax. Square brackets, [ ], indicate optional items.](https://masterofficevba.com/wp-content/uploads/2021/03/While_Wend_Statement_Syntaxnew-300x163.png)
![The Do – Loop Until statement’s syntax. Square brackets, [ ], indicate optional items while vertical bars, |, indicate mutually exclusive items.](https://masterofficevba.com/wp-content/uploads/2021/03/Do_Loop_Until_Statement_Syntaxnew-300x163.png)